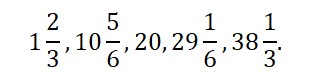Исторические задачи

 Исторические задачи, в которых обнаруживается арифметическая прогрессия 

Задача 1. Задача из  «Арифметики» Л.Ф. Магницкого

Купец имел 14 чарок серебряных, причем веса чарок растут по арифметической прогрессии с разностью 4. Последняя чарка весит 59 латов. Определить, сколько весят все чарки.

Решение

Ответ: все чарки весят 462 лата.

 

В «Сборнике алгебраических задач» (часть вторая, авторы Шапочников Н.А., Вальцов Н.К.; Москва, Ленинград, Учпедгиз, 1949) было найдено двадцать задач на арифметическую прогрессию.

Задача 2. Работники нанялись вырыть колодезь с таким условием, чтобы за первый аршин глубины им заплатили 40 копеек, а за каждый следующий         15-ю копейками больше, чем за предыдущий. Сколько аршин вырыли они, если за всю работу получили 16 р. 90 к.?

Решение:

Так как по условию задачи n>0, то n=13.

Работники выкопали колодец глубиной 13 аршин.

 

Задача 3. Некто, будучи должен 720 руб., обязался уплачивать этот долг по частям, выдавая каждый месяц 10-ю рублями меньше, чем в предыдущий. Сколько он уплатил в первый месяц и во сколько времени погасил весь свой долг, если в последний месяц ему пришлось отдать 40 р.?

Решение: Применим формулы n–го члена и суммы n первых членов арифметической прогрессии получим систему уравнений:   

         Так как n>0, то приходим к выводу, что свой долг человек вернул за 9 месяцев, отдав в первый месяц 120 рублей.

 

Задача 4. Древнейшая задача о делении хлеба. Сто мер хлеба разделить между пятью людьми так, чтобы второй получил на столько же больше первого, на сколько третий получил больше второго, четвёртый больше третьего и пятый больше четвертого. Кроме того, двое первых должны получить в 7 раз меньше трёх остальных. Сколько нужно дать каждому?

Решение:  Пусть у - разность арифметической прогрессии, тогда доля первого – х; доля второго – (х + у);  доля третьего – (х + 2у); доля четвертого – (х + 3у); доля пятого – (х + 4у). Затем составим систему уравнений:

Следовательно, хлеб должен быть разделен на следующие части:

Задача 5. За 16 дней Карл украл у Клары 472 коралла. Каждый день он крал на 3 коралла больше, чем в предыдущий день. Сколько кораллов украл Карл в последний день?

Решение:

Ответ: 52 коралла украл Карл в последний день.

Задача 6: Лестница имеет 100 ступеней. На первой ступени сидит 1 голубь, на второй – два, на третий – три. Так на всех ступенях до сотой. Сколько всего голубей?

Решение:

Ответ: 5050 голубей.